
DonCorson
[AHCI]
3358

Approaching Resonance - part 3
Approaching Resonance - part 3
Don Corson, December 2013
This is the third of a series discussing the behaviour of so called “resonant” watches. As we have seen these watches are properly called watches with coupled oscillators.
Click here to read the first instalment of this series, click here to read the second instalment.
This image from the second instalment shows the general scheme of the coupled oscillator “resonant” watch that I am investigating. The coupling between the two oscillators is through the movement of the hairspring studs that are attached to a coupling spring.
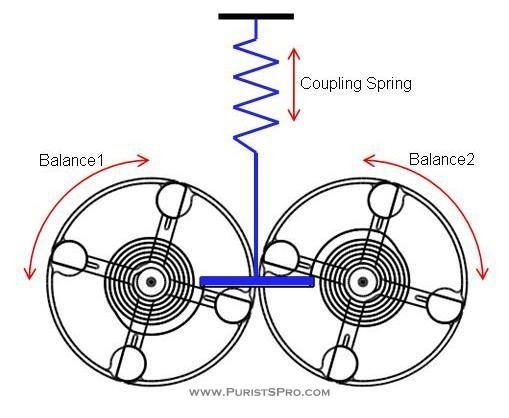
Figure 1
I finished the last instalment of this series showing how two out-of-phase oscillators with the same natural frequency get back in phase when they are coupled. Now let’s continue by looking at the results of the simulations for two oscillators with differing natural frequencies and how they behave when they are resonantly coupled.
In the diagram below we see the two oscillators starting out, each at its own natural frequency, and how their frequencies converge over time. One of the oscillators is at 4Hz, the other at about 4.0055Hz (that makes approx. 475 seconds a day fast). As we see, through the resonant coupling they both take on a frequency of about 4.00275Hz, or the average of the two natural frequencies.
Through the use of a simple coupling spring we have achieved the same result as through the use of a differential with its many parts and corresponding losses that also requires much space in the movement. The differential does have one advantage. It will average any two frequencies, no matter how far apart they are. This is not possible with resonant coupling. When the natural frequencies of the two oscillators are too far apart they will not converge.

Figure 2
In Figure 2 we can see a possible problem with resonant coupling in a watch. The amplitude of the slower balance increases, in this case it would probably cause banking. But remember that this is a case where the balances are timed almost 8 minutes a day differently. We can do better than that. At about 4.5 minutes a day difference things are already more manageable as we see below:

Figure 3
Finally at about 1 minute a day timing difference the simulation shows us this.

Figure 4
And we will see to it that our timing difference between the two balances will be much, much better than that.
Now let us take a look at the difference in behaviour of coupled and non-coupled systems to a rotating disturbance. The situation is this; I start the oscillators with a series of different phase differences. After 60 seconds the watch is rotated 45° in 0.4 seconds, after 3 seconds it is rotated back to the original position. After twenty seconds the same is done with the rotation in the other direction. The deciding difference between coupled and uncoupled systems is that the phase difference between the balances of the coupled system will in general always be the same. In a non-coupled system the phase difference can over time take on any value. Let us look at the difference in how the coupled and non-coupled systems react. The graphs from the simulations show the average amplitude of the two balances.

Figure 5
In the case without coupling we can see that the system reaction to the disturbance depends on the phase difference between the balances at the time of the disturbance. As this phase difference can and does change when the system isn’t coupled the reaction of the system changes too.

Figure 6
As the resonant coupled system tries to maintain the phase difference between the balances constant the reaction of the system is almost identical in all the cases. Despite the fact that the oscillators were started with a phase difference each time, the 60 seconds before the disturbance is enough that the phase difference is almost 0 by the time of the disturbance. Note that the coupled graphic shows the same number of simulations with the same initial conditions as the non-coupled graphic. As the results of the simulations for the coupled system are almost identical every time we see only one line.
I also tried to simulate the effects of a shock, a short sudden increase in the friction in the bearings of the balance axle. For this case I did not see a significant difference between the coupled and non-coupled systems.
I like to imagine that these differences I did see to rotative disturbances will make the resonant coupled system show better timing results when worn on the arm, but can not show it with these simulations. There are differences in frequency for short periods during the disturbances, but they are too small in comparison to the simulation noise for me to make any conclusions. Practical tests will have to show if there is a difference.
My conclusion to these simulations is that there is a difference in the behaviour of coupled and non-coupled multi-oscillator systems. This difference in behaviour is related to the fact that the coupled oscillators have a more or less fixed phase difference. In a non-coupled system the phase difference can take on any possible value at different times. The reaction of the system depends on the phase difference at the time of the disturbance. At a certain phase difference the errors caused by the disturbance are cancelled out. Happily, the coupled system tries to always resonate with such a phase difference.
The non-answered question is if this difference is significant when the watch is being worn under real-life conditions. I hope that I will be able to answer this question in the future when I have my next watch finished. I have planned to make 2 coupling springs. One according to the values I have chosen here for the coupled system and a second one that will just be fixed and as such allow no coupling. Then I should be able to do an “on-the-arm” test. I am looking forward to sharing the results, but please be patient.


This message has been edited by DonCorson on 2013-12-26 05:01:40

Approaching Resonance - part 3

"The plot thickens" ...

Looking forward to the results of the result...

I've been saving your resonance posts for...

"fixed"?
