
DonCorson
[AHCI]
3358

WatchTech101.2 - Main Spring Curvature
WatchTech101.2 - Main Spring Curvature
It is always interesting to see the beautiful curve of a main spring when removed from the barrel. It looks like it was drawn by an artist looking for a beautiful organic form. But it is, as so often, not an eye with good taste that determined the form, but the hard look of geometry meeting materials science.
Let's take a look inside a watch barrel in more detail. Below we see a fully wound main spring inside its barrel. We can see that the main spring is wound around the axle in the center. The main spring forms a spiral with tight inner windings and larger outer windings, with all the sizes in between.

Just to simplify things a little for our calculations let us assume that the windings of the spring are concentric loops around the central axle. From one loop to the next the radius increases by the thickness of the spring. This configuration is much easier to calculate and the error is still very small. We see clearly that each loop has a different radius and resulting from that a different circumference or length.
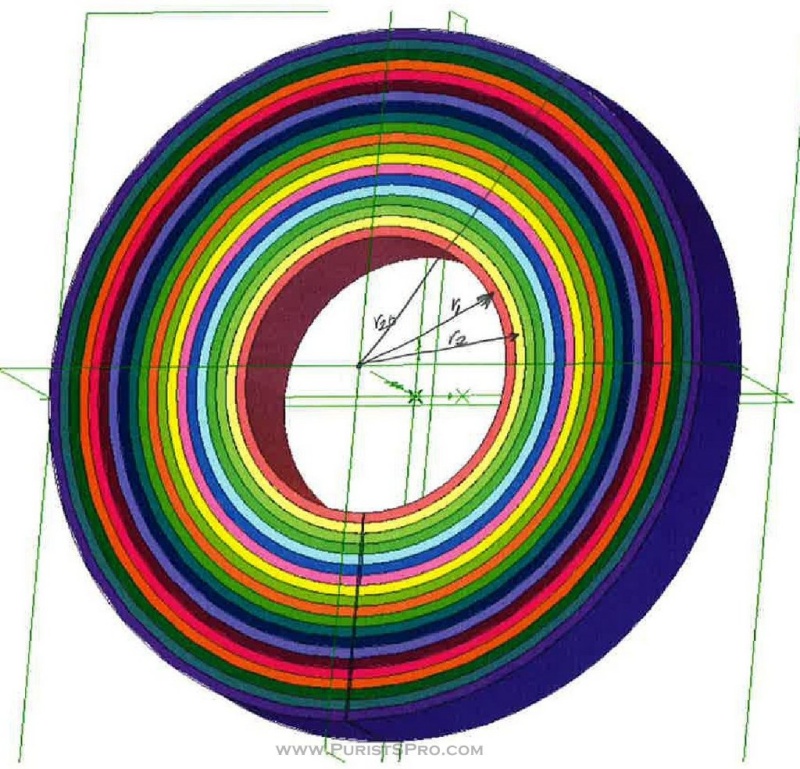
We see immediately that the inner most coil is bent the most, it has the smallest radius. Thus it has the highest material stress. The amount of stress a spring can accept without it taking on a new shape is described by the elastic limit
?max. The angle that a barrel spring will bend at the elastic limit is given by the following formula:
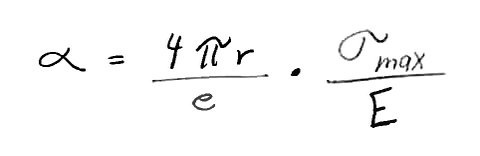
with
?=angle the spring can be bent.
r=the radius of the bend
e=thickness of the spring
?max=elastic limit of the spring material
E=module of elasticity of the spring material
What does this formula tell us? Assuming that the spring material (which determines ?max and E) is given:
1) If r (radius of the bend) decreases the bending angle decreases
2) If e (the thickness of the spring) increases the bending angle decreases
So to have a big bending angle we need a thin spring with a large radius for the bend, both things that we don’t really want. We would prefer to have a thicker spring to store more energy and a small radius so the spring does not become too large.
For a watch barrel using a straight spring and a constant thickness we would have to design such that the innermost loop, which has the smallest radius and thus the highest material stress and the smallest bending angle, has the spring material at the elastic limit. Each further loop would have a lower value of stress as the radius gets larger with each loop.
Below we see the formula for the potential energy of a spring. As we can see if ?, the stress, is reduced the potential energy is also reduced, and on top of that it is reduced exponentially.
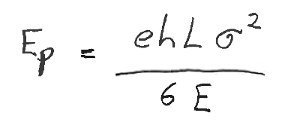
This drastically reduces the amount of energy available from the spring. As the barrel unwinds each coil is bent less, i.e. is farther away from being bent to the elastic limit. However, to store the most energy we would like to have each coil bent as much as possible, bent to the elastic limit.
So how can we achieve having the entire length of the spring being bent to the elastic limit?
The answer is; we give the relaxed spring a form such that each loop of the coil is bent enough so the bending from winding will bring the stress in the metal just up to the elastic limit. Expressed differently; each complete loop is 360°. If the angle the spring can be bent is limited by the elastic limit to, for example, 195° we preform the spring to be bent the rest of the 360°. For this example it would thus be preformed to a 165° bend.
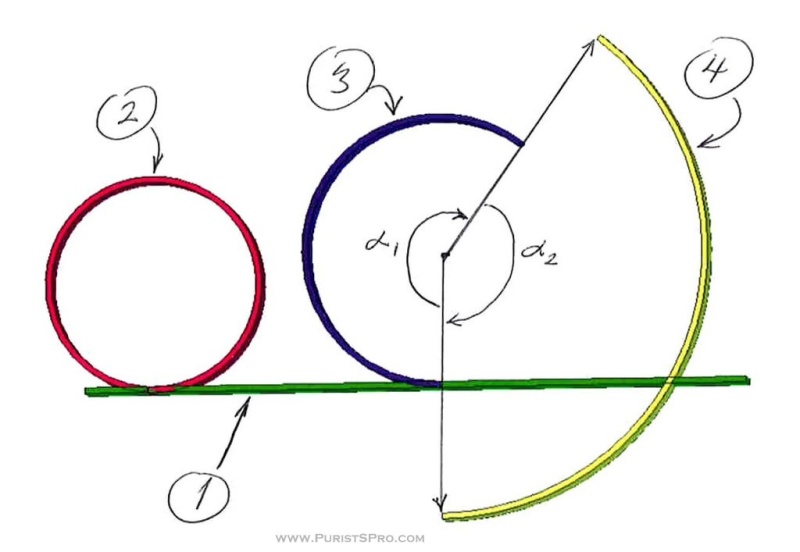
To visualise this take a look at the diagram below.
The straight spring is at (1), the diameter of the loop at (2), the length of (1) is the same as the circumference of (2). Let’s say that our spring can only be bent by the angle ?1 before reaching its elastic limit (3). To be able to make the complete loop as (2) we need to preform the spring like at (4). Note that each of these figures in the diagram have the same circumference or length, they symbolise the same piece of spring. As they have a constant circumference/length the radii of the arcs changes depending on the included angle.
Let's see what comes out if we pop some values into the above formula for the maximum bending angle for a given spring. Let's use the following values which are rather generic, but close to what you will find in the barrel of your watch:
e=thickness of the spring=0.128 mm
l=length of the spring=400 mm
h=height of the spring=1.15 mm
?max=elastic limit of the spring material=3400 N/mm2
E=elastic module of the spring material=200’000 N/mm2
r1=radius of the innermost coil of a spring=1.17 mm
r20=radius of the outermost coil of a spring=r1 + (19 * e)=4.13mm
Getting out our calculator we see that for the innermost loop ?1 is 168° while for the outermost loop ?20 is 401°, more than once around. To get the stress on the entire length of the spring to the elastic limit ?max we need to preform the innermost part of the coil more than half way around to keep it from deforming when wound, while the outermost coil needs to be bent backward by 41° to increase the material stress to the limit.
If we do this calculation for all the 20 coils of this spring we will find that there is a different form for each loop of the coil. In the diagram below we can see the 20 loops of the coil, each with its length and preformed curvature.

If we then take these portions of the coil and put them end to end we will get the final length and form of the spring.

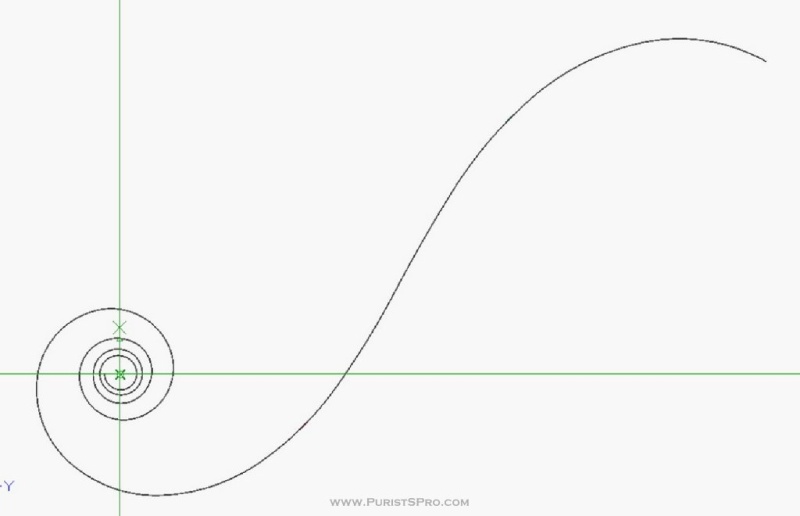
Have you seen this form before?

(Note that the Y at the end of this 2824-2 main spring is caused by the bridle. The bridle is a second spring in the barrel that presses the end of the main spring onto the barrel wall. The outer end of the mainspring is fixed not by a hook, but by friction. If the spring is wound too much by the automatic winding mechanism the end of the spring slips against the barrel wall preventing deformation/destruction of the main spring.)
For a more detailed discussion of barrel springs and their calculation see:
Traité de construction horlogère
Michel Vermot, Philippe Bovay, Damien Prongué, Sébastien Dordor, Vincent Beux
Presses polytechniques et universitaires romandes, Lausanne
2011
ISBN: 978-2-88074-883-8
1120 pages
or
Théorie général de l’horlogerie
Léopold Defossez
La Chambre suisse de la horlogerie, La Chaux-de-Fonds
1950




